如何判断点在多边形内

发表于 | 分类于 |

最近逛知乎的时候，看到轮子哥说了一句话，如何判断一个点在凸多边形里，对于任何计算机专业出来的人来说，都应该跟妈妈的脸一样永远记在心里。这话一听就很有道理，特别是在游戏开发中，这是经常需要用到的，例如Navigation Mesh的生成。

于是乎，为了记住妈妈的脸（误），我查阅了相关资源，学习了一下相关的算法。

相关资料如下：

如何判断2个线段相交
几何-判断点在多边形内部
数学美之判断线段相交的最简方法
判断一个点是否在多边形内部 [2] 射线法实现

文章将先介绍一些基础的数学方法，然后分为几个部分记录如何判断点在多边形中，并用Unity实现相应的代码。

二维向量的叉积

二维向量的叉积可以用来判断两个向量的相对位置（左旋右旋）。

（x1, y1） × (x2, y2) = x1y2 - y1x2

如果值大于0，则(x2, y2)在(x1, y1)左边，反之则在右边。

1
2
3
4
5
6
7
8
9
public static class ExtensionMethods{

	/// <summary>
	/// Cross product of two Vector2
	/// </summary>
	public static float Cross(this Vector2 v1, Vector2 v2){
		return v1.x * v2.y - v1.y * v2.x;
	}
}

如何判断两个线段相交

判断两线段相交的方法，在网上看了很多资料，找到了相对不错的方法，通过向量跨立实验来判断。

大致思想就是，如果一条线段跨越了另一条线段，那么被跨越线段的两个端点应该在这条直线两边。也就是说，如果两条线段分别是(A, B)和(C, D)。那么AC x AB和AD x AB应该异号（或者为零）。同样，BC x BA和BD x BA也应该异号（或为零）。

这基本满足了大部分情况的判定，唯有一种特殊情况需要考虑一下。如果两条线段平行但不相交，此时上述的判定条件是满足的（都为零）。因此，我们在做跨立实验之前可以多一步判断，通过判断两个线段在x轴和y轴上的投影是否相交来做一步简单的判断，如果不相交，则两线段一定不相交。

1
2
3
4
5
6
7
8
9
10
11
12
13
public static bool CheckLineSegmentCross(Vector2 a, Vector2 b, Vector2 c, Vector2 d){
  // First check
  if(Mathf.Max(a.x, b.x) < Mathf.Min(c.x, d.x) || Mathf.Min(a.x, b.x) > Mathf.Max(c.x, d.x)
  || Mathf.Max(a.y, b.y) < Mathf.Min(c.y, d.y) || Mathf.Min(a.y, b.y) > Mathf.Max(c.y, d.y))
    return false;

  // Second check
  if((c - a).Cross(b - a) * (d - a).Cross(b - a) <= 0
  && (c - b).Cross(a - b) * (d - b).Cross(a - b) <= 0)
    return true;
  else
    return false;
}

如何判断一个点在凸多边形内

对于判断一个点在凸多边形内，有多种方法，这里简要介绍一下旋转法和内角和法，然后重点研究一下射线法。

旋转法

对于一个凸多边形，我们可以先对多边形的顶点集沿顺（逆）时针排序，然后依次得到目标点到每一个定点的向量集。若目标点在多边形内，则相邻两个向量的叉积同号。

内角和法

如果一个点在凸多边形内，那么目标点和所有相邻顶点构成的所有夹脚的和应该为360度。

射线法

以上两种方法都只局限于凸多边形，若是凹多边形，上述方法并不适用。那么我们就要用到射线法了。

若一个点在一任意多边形中，则从该点沿任意方向射出一条射线，射线与多边形的交点个数为奇数。

这其实很明显，每产生一个交点，证明射线进入（或离开）多边形内部。若点在多边形内部，而射线的终点（无限远）一定在多边形外部，因此交点的个数只能是偶数。

这里需要解决几种特殊情况。

  1. 点在多边形边上
  2. 点在多边形顶点上
  3. 射线经过多边形顶点
  4. 射线经过多边形的一条边

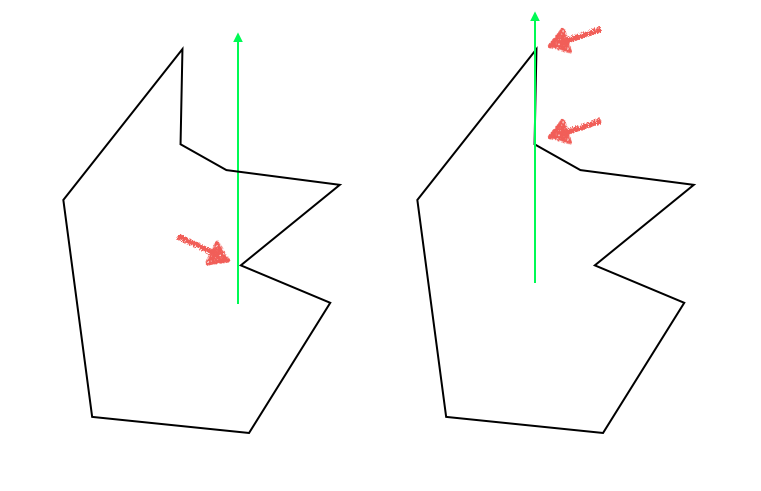
其中，1和2相对来讲较为容易解决，只需要简单地判断点在边上和点与顶点重合即可，相对来讲较难处理的是3和4。我参考了网上一些相关的教程（然后发现很多都有一定的错误=。=），其中较好的一个判断方法是，规定射线经过的点都属于射线以上的一侧，而若发生顶点跨立，则要求被跨立线段的两个顶点在原线段两侧，这样就解决了射线经过多边形顶点的问题。而4属于3的特殊情况，一样可以通过这个方法去判断。

如上图所示，X射线穿越了两次，Y射线穿越了一次，Z射线没有发生穿越，因此只有点Y在多边形内。

但这些方法实现起来较为麻烦，比如在顶点跨立这里，需要先判断发生了顶点跨立，然后再去判断两个顶点关于原线段的相对位置，相应的代码实现也较为复杂。于是我试着发掘有没有更加简便的方法。这里我想的是，考虑到我们是随机选择一条射线，实际上情况3和情况4发生的概率是非常低的。那么，如果真的发生了3和4的情况，我们重新选择一条射线不就好了，这样无论是从代码复杂度上或者是逻辑上都变得简单不少。我们不去考虑极特殊情况的处理，鉴于其概率非常低，真发生了重跑就好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static bool CheckPointInPolygon(Vector2 p, Vector2[] vertices){
		Vector2 pFar = Random.insideUnitCircle * float.MaxValue;
		int crossCount = 0;

		for(int i = 0; i < vertices.Length; i++){
			Vector2 a = vertices[i];
			Vector2 b = i == vertices.Length - 1 ? vertices[0] : vertices[i + 1];

			// Check point on line segment
			if(CheckPointOnLineSegment(p, a, b))
				return true;

			// 1. Check point parallel to line
			// 2. Check vertex on ray
			if((pFar - p).Cross(b - a) == 0 || Math.CheckPointOnLineSegment(a, p, pFar))
				return CheckPointInPolygon(p, vertices);

			// Check point cross the line
			if(Math.CheckLineSegmentCross(p, pFar, a, b))
				crossCount += 1;
		}

		if(crossCount % 2 != 0)
			return true;
		else
			return false;
	}