In this chapter we introduce Finite Markov Decision Process. Different from last chapter of k-armed bandits problem, we will move deeper — to choose different actions in different situations.
Definition
MDPs are a classical formalization of sequential decision making, where actions influence not just immediate rewards, but also subsequent situations, or states, and through those future rewards.
- Agent: The learner and decision maker.
- Environment: The thing the agent interacts with, comprising everything outside the agent.
These interact continually, the agent selecting actions and the environment responding to these actions and presenting new situations to the agent. The environment also gives rise to rewards, special numerical values that the agent seeks to maximize over time through its choice of actions.
More specifically, the agent and environment interact at each of a sequence of discrete time steps, $t=0,1,2,3,….$. At each time step t,the agent receives some representation of the environment’s state, $S_t ∈ \mathcal{S}$, and on that basis selects an action, $A_t ∈ \mathcal{A}(s)$. One time step later, in part as a consequence of its action, the agent receives a numerical reward, $R_{t+1} ∈ \mathcal{R} ⊂ \mathbb{R}$, and finds itself in a new state, $S_{t+1}$.
The MDP and agent together thereby give rise to a sequence or trajectory that begins like this:
$S_0, A_0, R_1, S_1, A_1, R_2, S_2, …$
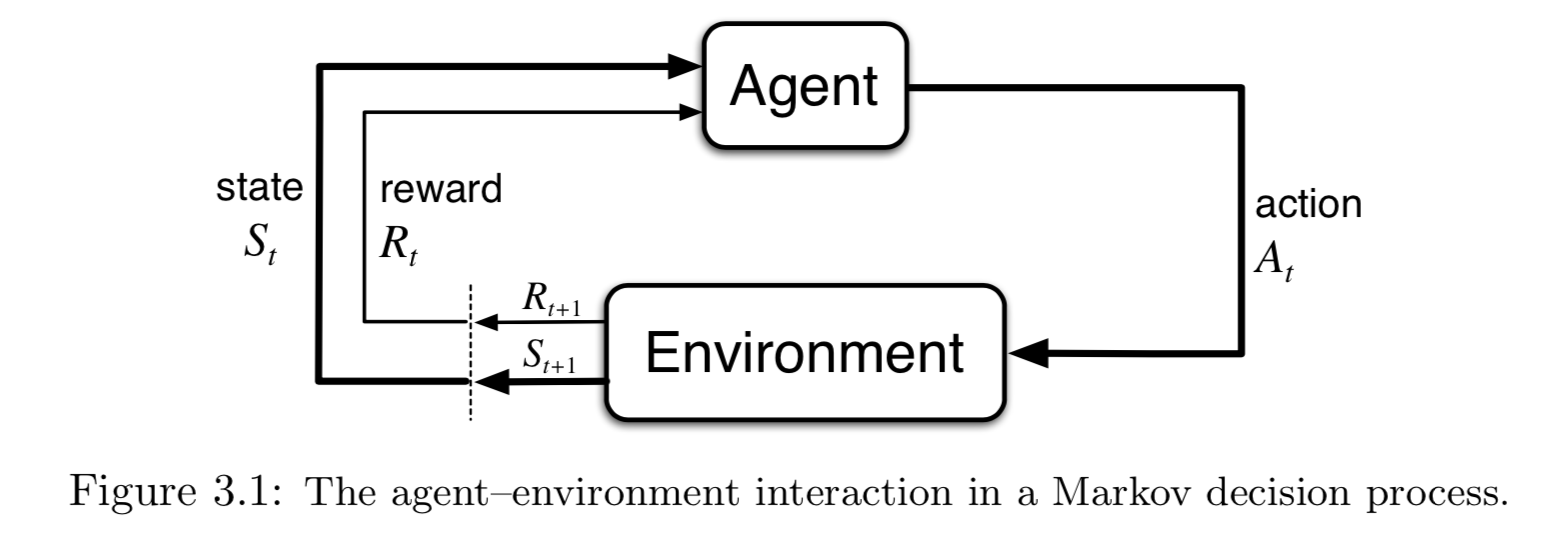
In finite MDP, the sets of states, actions, and rewards all have a finite number of elements.
In this case, the random variables Rt and St have well defined discrete probability distributions dependent only on the preceding state and action, which is also named Environment Dynamics:
$p(s^{‘}, r|s, a) = Pr\{S_t = s^{‘}, R_t = r | S_{t-1} = s, A_{t-1} = a\}$
From the function p, we can also compute other things about the environment.
- State-transition probabilities : $p(s^{‘} | s, a) = Pr\{S_t = s^{‘} | S_{t-1} = s, A_{t-1} = a\}$
- Expected rewards for state-action pairs : $r(s, a) = \mathbb{E}[R_t | S_{t-1} = s, A_{t-1} = a]$
- Expected rewards for state-action-next-state triples: $r(s^{‘}, s, a) = \mathbb{E}[R_t | S_t = s^{‘}, S_{t-1} = s, A_{t-1} = a]$
An Example — Recycling Robot
A mobile robot has the job of collecting empty soda cans in an office environment. It has sensors for detecting cans, and an arm and gripper that can pick them up and place them in an onboard bin; it runs on a rechargeable battery. The robot’s control system has components for interpreting sensory information, for navigating, and for controlling the arm and gripper. High-level decisions about how to search for cans are made by a reinforcement learning agent based on the current charge level of the battery. This agent has to decide whether the robot should (1) actively search for a can for a certain period of time, (2) remain stationary and wait for someone to bring it a can, or (3) head back to its home base to recharge its battery. This decision has to be made either periodically or whenever certain events occur, such as finding an empty can. The agent therefore has three actions, and the state is primarily determined by the state of the battery. The rewards might be zero most of the time, but then become positive when the robot secures an empty can, or large and negative if the battery runs all the way down. In this example, the reinforcement learning agent is not the entire robot. The states it monitors describe conditions within the robot itself, not conditions of the robot’s external environment. The agent’s environment therefore includes the rest of the robot, which might contain other complex decision-making systems, as well as the robot’s external environment.
Goals and Rewards
That all of what we mean by goals and purposes can be well thought of as the maximization of the expected value of the cumulative of a received scalar signal (called reward).
As we can see, here we are going to maximize not immediate rewards, instead long-term ones.
The agent always learns to maximize its reward. If we want it to do something for us, we must provide rewards to it in such a way that in maximizing them the agent will also achieve our goals.
Here we can give a typical example. A chess-playing agent should be rewarded only for actually winning, not for achieving subgoals such as taking its opponent’s pieces or gaining control of the center of the board. If achieving these sorts of subgoals were rewarded, then the agent might find a way to achieve them without achieving the real goal. For example, it might find a way to take the opponent’s pieces even at the cost of losing the game.
The reward signal is your way of communicating to the robot what you want it to achieve, not how you want it achieved.
Returns and Episodes
If the sequence of rewards received after time step t is denoted $R_{t+1}, R_{t+2}, R_{t+3}, …$, then we seek to maximize the expected return, denoted $G_t$, defined as cumulative of rewards in long run:
$G_t = R_{t+1} + R_{t+2} + R_{t+3} + … + R_T$
where $T$ is a final time step.
This approach makes sense in applications in which there is a natural notion of final time step, that is, when the agent–environment interaction breaks naturally into subsequences, which we call episodes. Each episode ends in a special state called the terminal state, followed by a reset to a standard starting state or to a sample from a standard distribution of starting states.
Tasks with episodes of this kind are called episodic tasks. In episodic tasks we sometimes need to distinguish the set of all nonterminal states, denoted $\mathcal{S}$, from the set of all states plus the terminal state, denoted $\mathcal{S}^{+}$. The time of termination, $T$, is a random variable that normally varies from episode to episode.
We will also have continuing tasks, which the agent-environment interation can not break naturally into identifiable episodes, but goes on continually without limit ($T = \infty$)
Here we give some examples to show the difference between episodic tasks and continuing tasks. For a chess game, it will finally end and restart, which is a typical episodic tasks. For an on-going process-control task or an application to a robot with a long life span, we don’t know when it will terminate.
Using sum of rewards in continuting tasks will easily be infinite (which does not converge). Instead of we use discounted return:
$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + … = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}$
where $\gamma$ is a parameter, $0 \leq \gamma \leq 1$, called the discount rate. As $\gamma$ approaches 1, the return object takes future rewards into account more strongly, therefore the agent becomes more farsighted.
Returns at successive time steps are related to each other in a way that is important for the theory
and algorithms of reinforcement learning:
$G_t = R_{t+1} + \gamma G_{t+1}$
By introducing a special absorbing state that transitions only to itself and that generates only rewards of zero, we can combine episodic tasks and continuing tasks together.

$G_t = \sum_{k=t+1}^{T} \gamma^{k-t-1} R_k$
including the possibility that $T = \infty$ or $\gamma = 1$ (but not both).
Policies and Value Functions
Almost all reinforcement learning algorithms involve estimating value functions — functions of states (or of state–action pairs) that estimate how good it is for the agent to be in a given state (or how good it is to perform a given action in a given state).
Formally, a policy is a mapping from states to probabilities of selecting each possible action. If the agent is following policy $\pi$ at time t, then $\pi(a|s)$ is the probability that $A_t = a$ if $S_t = s$. Reinforcement learning methods specify how the agent’s policy is changed as a result of its experience.
The value of a state s under a policy π, denoted $v_{\pi}(s)$, is the expected return when starting in s and following π thereafter. For MDPs, we can define $v_{\pi}$ formally by:
$v_{\pi}(s) = \mathbb{E}_{\pi}[G_t | S_t = s]$, for all $s \in \mathcal{S}$,
where $\mathbb{E}[.]$ denotes the expected value of a random variable given that the agent follows policy $\pi$, and t is any time step. Note the the value of the terminal state, if any, is always zero. We called the function $v_{\pi}$ the state-value function for policy $\pi$.
We also have the action-value function for policy $\pi$ as following:
$q_{\pi}(s,a) = \mathbb{E}_{\pi}[G_t | S_t = s, A_t = a]$
For any policy $\pi$ and any state s, the following consistency condition holds between the value of s and the value of its possible successor states:
$v_{\pi}(s) = \sum_{a} \pi(a|s) \sum_{s^{‘}, r} p(s^{‘},r|s,a)[r + \gamma v_{\pi}(s^{‘})]$, for all $s \in \mathcal{S}$,
which is the Bellman equation for $v_{\pi}$. It expresses a relationship between the value of a state and the values of its successor states.
The value functions $v_{\pi}$ and $q_{\pi}$ can be estimated from experience using Monte Carlo methods, which we will discuss in Chapter 5.
Optimal Policies and Optimal Value Functions
Solving a reinforcement learning task means, roughly, finding a policy that achieves a lot of reward over the long run. That’s to find an optimal policy.
A polity $\pi$ is defined to be better than or equal to a policy $\pi^{‘}$ if its expected return is greater than or equal to that of $pi^{‘}$ for all states.
There is always at least one policy that is better than or equal to all other policies. They share the same state-value function, called the optimal state-value function, denoted $v_{\ast}$, and defined as:
$v_{\ast}(s) = max_{\pi} v_{\pi}(s)$, for all $s \in \mathcal{S}$
They also share the same optimal action-value function, denoted $q_{\ast}$, and defined as:
$q_{\ast}(s,a) = max_{\pi} q_{\pi}(s,a)$ for all $s \in \mathcal{S}$ and $a \in \mathcal{A}(s)$.
We can also write $q_{\ast}$ in terms of $v_{\ast}$ as follows:
$q_{\ast}(s,a) = \mathbb{E}[R_{t+1} + \gamma v_{\ast}(S_{t+1}) | S_t = s, A_t = a]$
Like Bellman equation, $v_{\ast}$’s consistency condition can be written in a special form without reference to any specific polity, which is called Bellman Optimality equation. Intuitively, the Bellman optimality equation expresses the fact that the value of a state under an optimal policy must equal the expected return for the best action from that state:
$v_{\ast}(s) = max_{a \in \mathcal{A}(s)} q_{\pi_{\ast}}(s, a) = max_a \sum_{s^{‘}, r} p(s^{‘}, r | s, a)[r + \gamma v_{\ast}(s^{‘})]$
Once we have $v_{\ast}$, we can give some other definition to optimal policy. Any policy that assigns nonzero probability only to these actions is an optimal policy. Or we can say, any policy that is greedy with respect to the optimal evaluation function $v_{\ast}$ is an optimal policy.
By explicitly solving the Bellman optimality equation, we are sure to obtain an optimal policy. However, this solution is rarely directly useful. This solution relies on at least three assumptions that are rarely true in practice:
- We accurately know the dynamics of the environment.
- We have enough computational resources to complete the computation of the solution.
- The model should satisfy Markov property.
Nowedays, the second condition is usually the bottleneck of reinforcement learning. Therefore, we should adopt some other decision-making methods to approximately solve the Bellman optimality equation, like heuristic search methods and dynamic programming, which we will discuss in next chapter.