This is the reading note after reading
Here is the part of the Chapter 8.
Navigation Graph Construction
When we want to apply a search algorithm in our game, we should first convert the pertinent spatial information into a graph-like data structure. There are different pupular methods utilized in modern games.
Tile Based
Each graph node represents the center of a cell, with the graph edges denoting the connections between adjacent cells. We will also use information of terrain type to weight the edges of the navigation graph accordingly.
The downside to using cells as the skeleton for a navgraph is that the search spaces can quickly become extremely large.
Points of Visibility
A points of visibility (POV) navigation graph is created by placing graph nodes, usually by hand, at important points in the environment such that each graph node has line of sight to at least one other.

One feature of POV graphs is that they may be easily expanded to include nodes that proffer information over and above the connectivity data. For example, nodes can easily be added to a POV graph to represent good sniping, cover, or ambush positions.
The downside is that if a game map is large and complex the map designer can spend an awful lot of precious development time positioning and tweaking the graph.
A POV graph can also be problematic if you plan to include any type of map generation feature, since you must then develop some automated method to generate the POV graph structure as well for the new maps to be of any use. One solution for this problem, however, is to use expanded geometry techniques.
Expanded Geometry
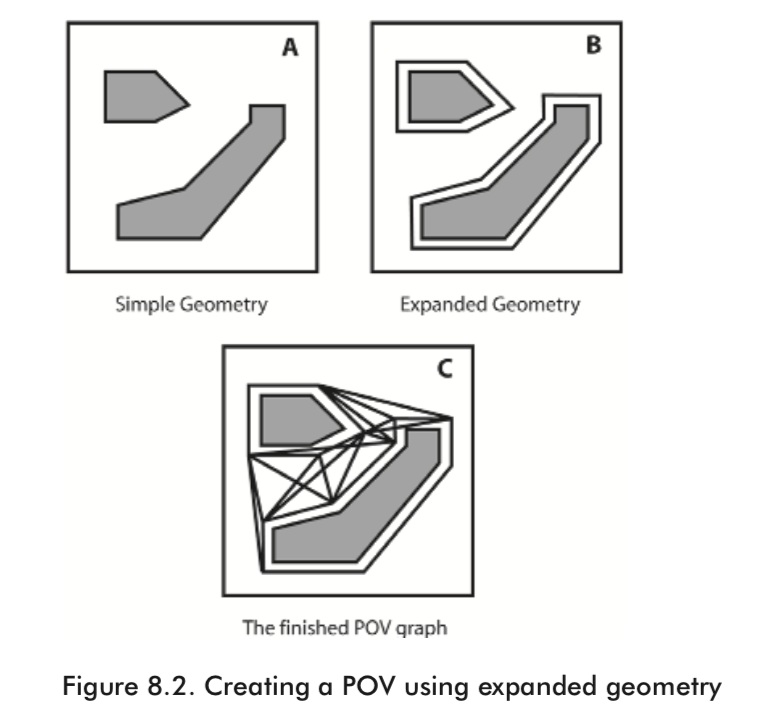
If a game environment is constructed from polygons it’s possible to use the information present in those shapes to automatically create a POV graph, which, for large maps can be a real time-saver. This is achieved by first expanding the polygons by an amount proportional to the bounding radius of the game agents. See Figures 8.2 A and B. The vertices defining this expanded geometry are then added as nodes to a navigation graph. Finally, an algorithm is run to test for line of sight between the vertices, and edges are added to the graph appropriately. Figure 8.2 C shows the finished navigation graph.
NavMesh
One approach growing in popularity with game developers is to use a network of convex polygons, called a navmesh, to describe the walkable areas of a game environment.
A convex polygon has the valuable property that it allows unobstructed travel from any point in the polygon to any other. This is useful because it enables an environment to be represented using a graph where each node represents a convex space (instead of a point).
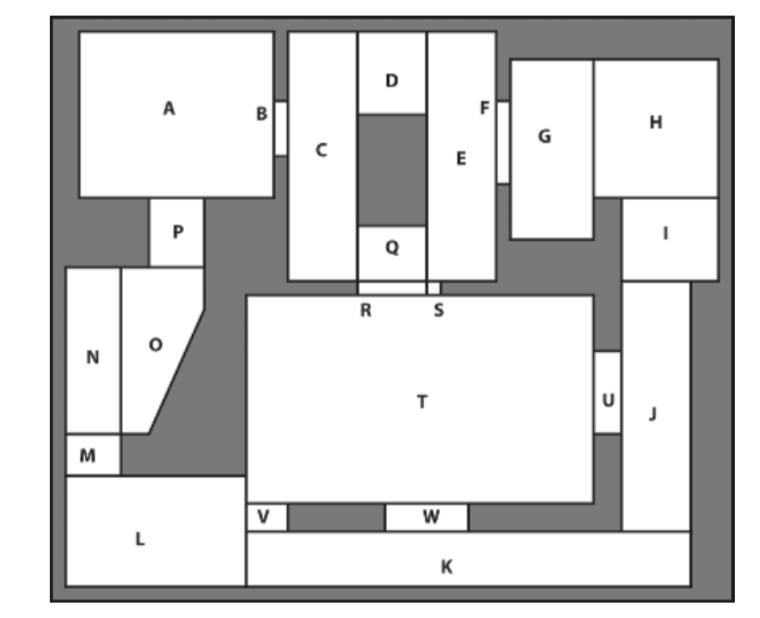
The advantage of navmesh:
- The data structure required to store one is compact and can be searched very quickly.
- It’s possible to use algorithms to partition the walkable areas of the maps automatically.
Granularity
Coarsely Granulated Graph
If a game restricts its agents to movement along the edges of a navigation graph only, such as the movement of the characters in the Pac-Man range of games , then a coarsely granulated navgraph is the perfect choice.

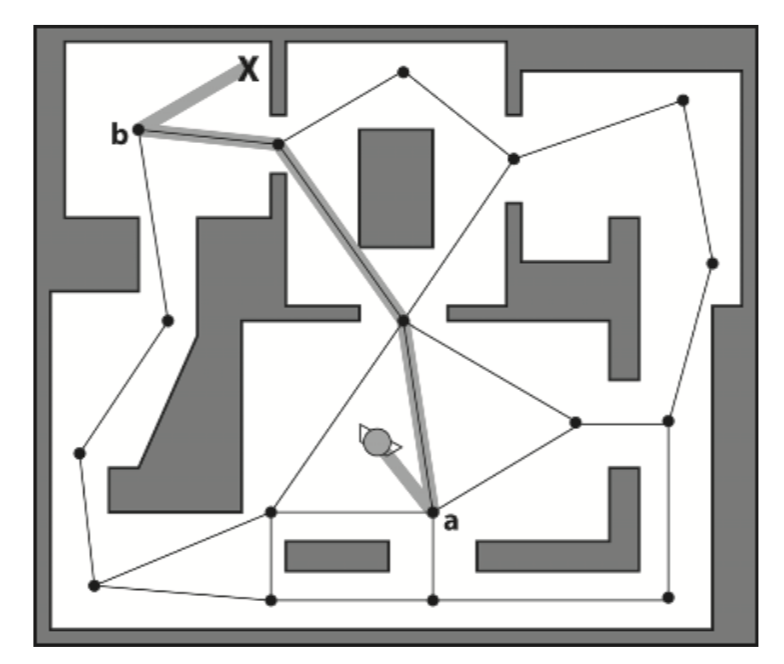
Notice that the agent may not be in the exact position of the node. So when we move the agent into position, the AI must do the following steps:
- Find the closest visible graph node to the NPC’s current location, say, node A.
- Find the closest visible graph node to the target location, say, node B.
- Use a search algorithm to find the least cost path from A to B.
- Move the NPC to node A.
- Move the NPC along the path calculated in step 3.
- Move the NPC from B to the target location.
However, the above steps have two drawbacks.
One is that due to the coarseness of the navigation graph there will still be many occasions where an agent will zigzag unnaturally at the start and end points of a path.
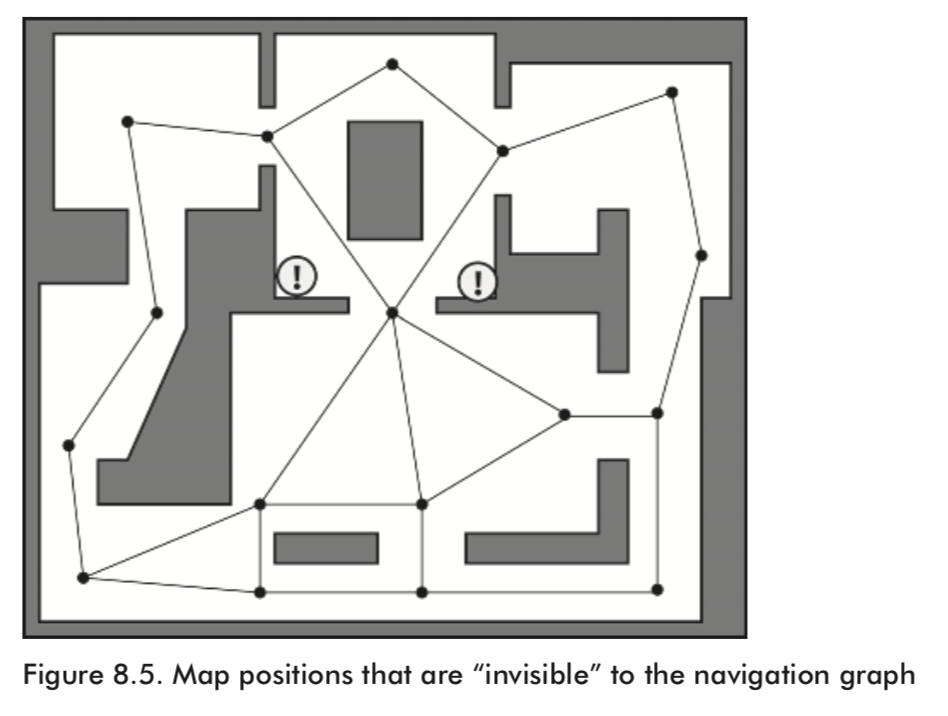
The other one is when using coarse graphs there are almost always a few positions on the map to which there is no line of sight from any of the graph nodes, effectively rendering those areas invisible to any path planner.
Finely Granulated Graph
Poor paths and inaccessible positions can be improved by increasing the granularity of the navigation graph.
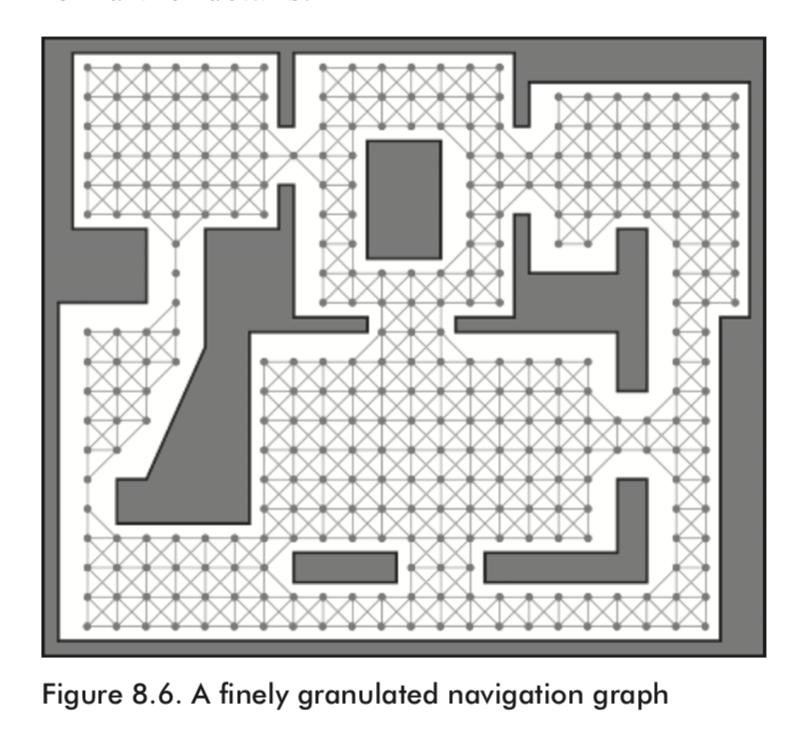
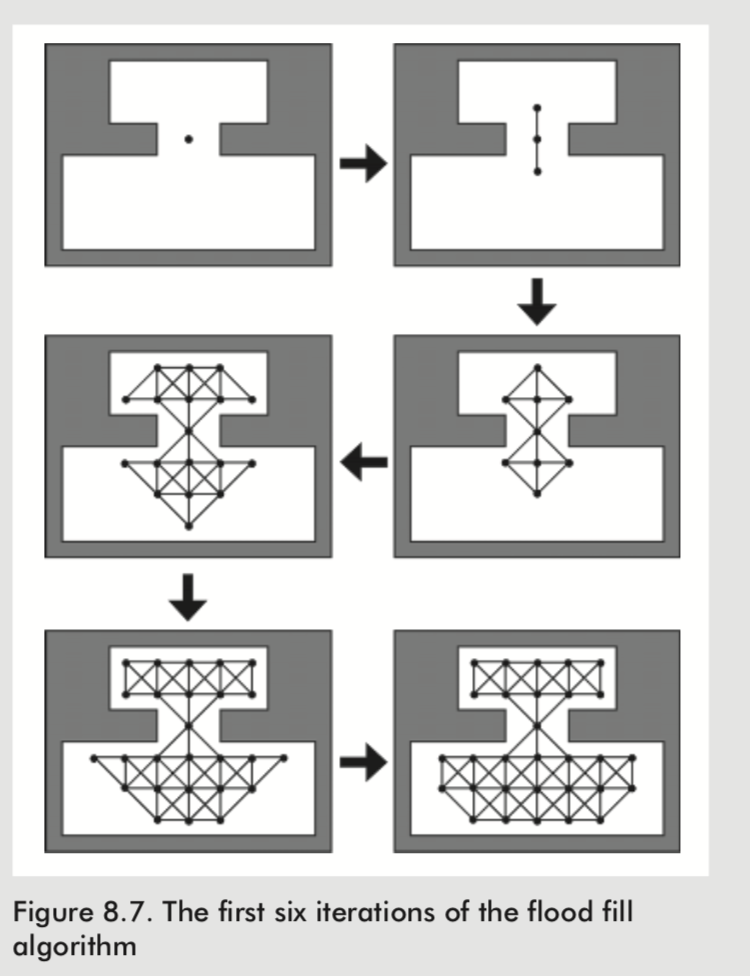
Creating a graph like this by hand is extremely tedious, so a flood fill algorithm is utilized by the map editor to do the majority of the work.
The detail of flood fill algorithm can be found in wiki.
Spatial Partitioning
Remember when we apply the pathfinding algorithm, we should firstly determine the closest visible node to a given position. If this search is undertaken by iterating through all the nodes in order to find the closest, the performance will be in O(n) time.
Instead, we can use spatial partitioning to speed up proximity queries. For navigation graphs of over a couple hundred nodes, spatial partitioning gives dramatic speed increases as the search time becomes a function of the node density, O(d), rather than the number of nodes; and since the density of nodes throughout navgraphs tends to be fairly consistent, the time taken to do a node proximity query will be constant.
Dijkstra in Item Searching
Usually the best way to search for the shortest path is AStar algorithm. However, supposed there are many instances of item in our game environment of the particular type. Consequently, when using A* to search for the closest instance of an item type, a search must be completed for each instance present in the game world before the one with the least cost path can be chosen as the best item to move toward. (e.g. it’s not uncommon for RTS game environments to include dozens or even hundreds of instances of resources like trees or gold.)
When many similar item types are present, Dijkstra’s algorithm is the better choice. As you’ve learned, Dijkstra’s algorithm “grows” a shortest path tree outward from the root node until either the target has been reached or the entire graph has been explored. As soon as the item searched for is located, the algorithm will terminate and the SPT will contain the path from the root to the closest item of the desired type. In other words, no matter how many instances of an item type are present in the game world, Dijkstra’s algorithm only needs to be run once to find the least cost path to one of them.
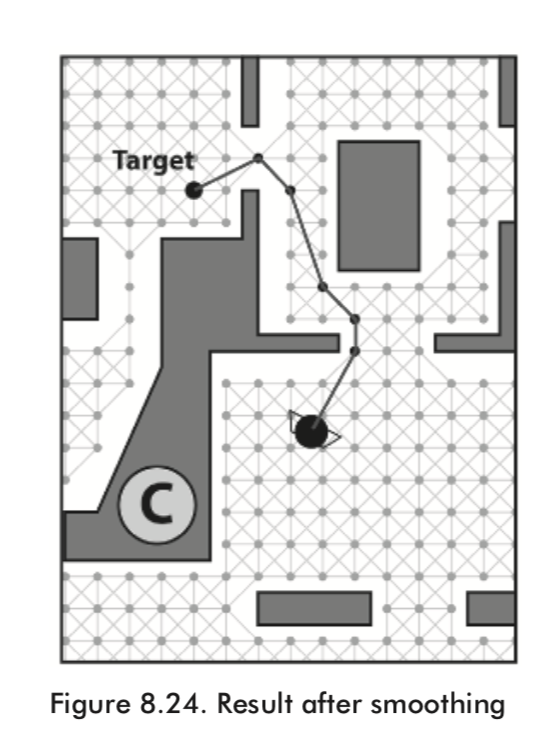
Path Smoothing
Quite often, and especially if a game’s navigation graph is in the shape of a grid, the paths created by the path planner tend to contain unnecessary edges, producing kinks like those shown in the following figure.
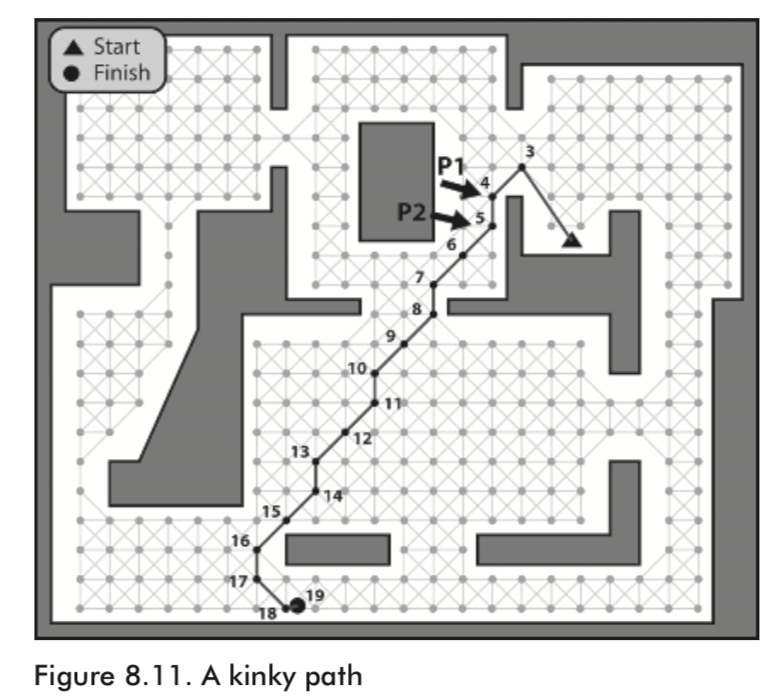
Path Smoothing Rough but Quick
A reasonably quick method for smoothing a path works by checking the “passability” between adjacent edges. If one of the edges is superfluous, the two edges are replaced with one.
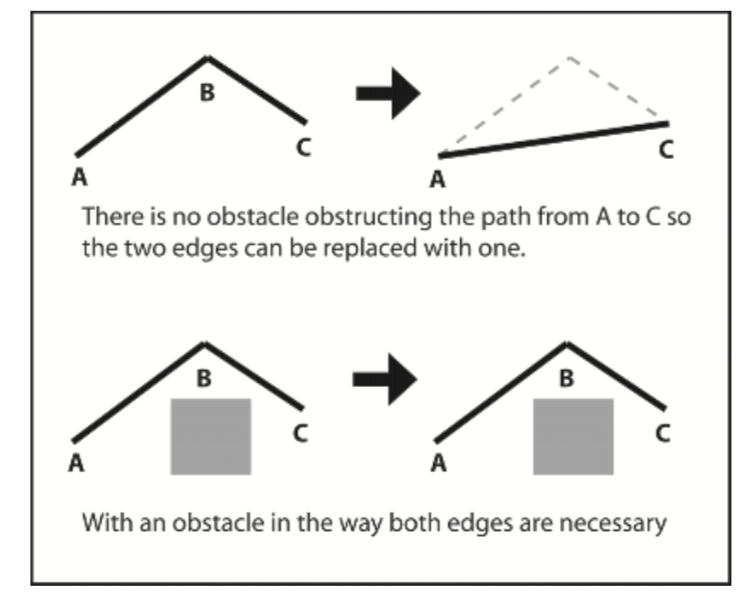
The algorithm proceeds as follows: First, two iterators, E1 and E2, are positioned at the first and second path edges respectively. Then these steps are followed:
- Grab the source position of E1.
- Grab the destination position of E2.
- If the agent can move between these two positions unobstructed by
the world geometry, assign the destination of E1 to that of E2 and remove E2 from the path. Reassign E2 to the new edge following E1. (Note that this is not a simple line-of-sight test as an entity’s size must be taken into consideration — it must be able to move between the two positions without bumping into any walls.) - If the agent cannot move unobstructed between the two positions, assign E2 to E1 and advance E2.
- Repeat steps until the destination of E2 is equal to the destination of the path.
Path Smoothing Precise but Slow
The previous algorithm is not perfect. The algorithm only checks the passability between adjacent edges, but not all pairs of edges. A more precise smoothing algorithm must iterate through all the edges from E1 to the final edge each time E1 is advanced. However, although precise, this method is much slower because many additional intersection tests have to be made.
Pay attention that some of the important edges cannot be deleted, like the bridge over a river.
Methods for Reducing CPU Overhead
If a game has oodles of AI controlled agents running around, all able to request paths at any time, then load spikes can occur when too many of them simulta- neously request searches. When this happens, the fluid flow of the game will be interrupted as the CPU attempts to keep up with the demands put on it, thus creating a jerky, stuttering motion. Therefore, we need to lessen the likelihood of load spikes by reducing the per-update overhead of path planning requests.
Precalculated Paths
If your game environment is static and you have memory to spare, a good option for lessening the CPU load is to use precalculated lookup tables, enabling paths to be determined extremely quickly.
This can be calculated using Dijkstra’s algorithm to create the shortest paths tree (SPT) for every node in the graph.
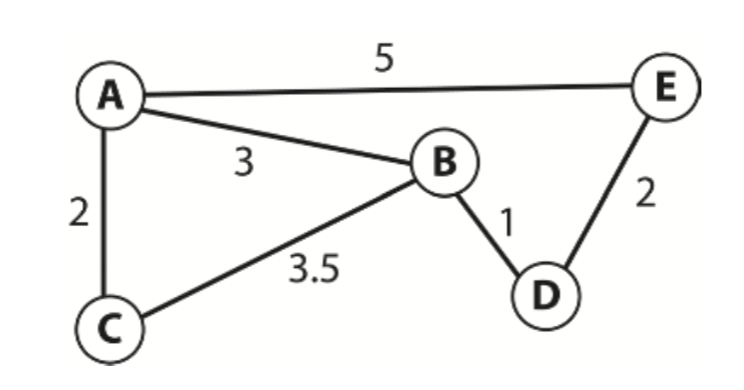
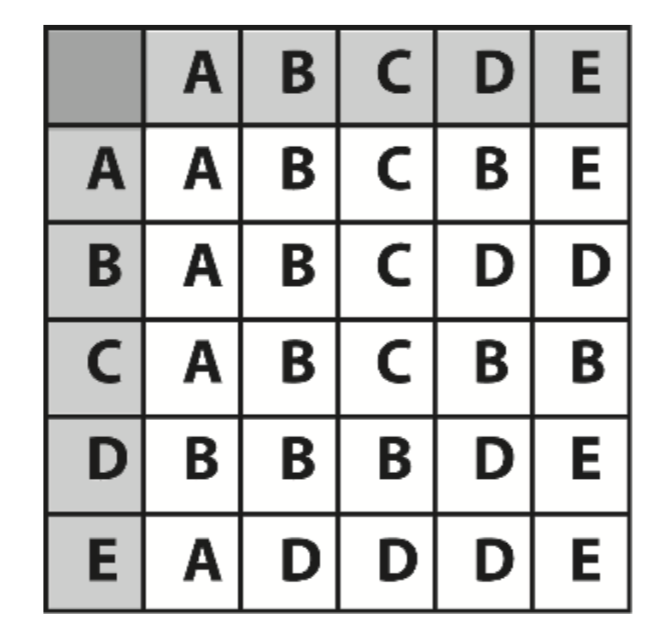
Precalculated Costs
Sometimes it’s necessary for a game agent to calculate the cost of traveling from one place to another. For example, together with other features, an agent may factor in the cost of a game object when deciding if it wants to pick up that item.
This is constructed in a similar way to the all-pairs route table discussed in the last section, except this time the elements of the table represent the total cost to follow the shortest path from one node to any other.
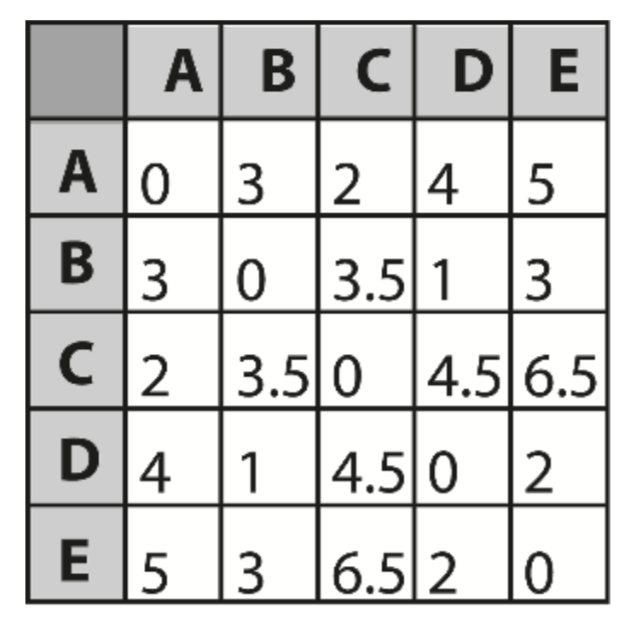
Time-Sliced Path Planning
An alternative to precalculating lookup tables to lighten the CPU load is to allocate a fixed amount of CPU resources per update step for all the search requests and to distribute these resources evenly between the searches. This is achieved by dividing up the searches over multiple time steps, a tech- nique known as time slicing.
First of all, the Dijkstra and A searches must be modified in such a way that they can search a graph over multiple update steps. Then, as agents request searches, their path planners create instances of the relevant searches (A or Dijkstra) and register themselves with a path manager class. The path manager keeps a list of pointers to all active path planners, which it iterates through each time step, evenly sharing the available CPU resources between them. When a search is either completed successfully or a path is not located, the path planner notifies its owner by sending it a message.
Preventing the Twiddling of Thumbs
One consequence of time-sliced path planning is that there will be a delay from the time an agent requests a path to the time it receives notification that the search has been successful or unsuccessful.
A simple option is for the agent to seek toward its goal until it receives notification from the search manager that a path is ready, at which time it follows the path. Or in the situation the bot requests a search to an item type, it simply wanders until it receives notification.
This works fine in most cases but it does present another problem: By the time a path is formulated, an agent may have moved quite a distance from the position where the search was initially requested. Consequently, the first few nodes of the path returned from the planner will be located in such a way that the agent will need to backtrack to follow them.
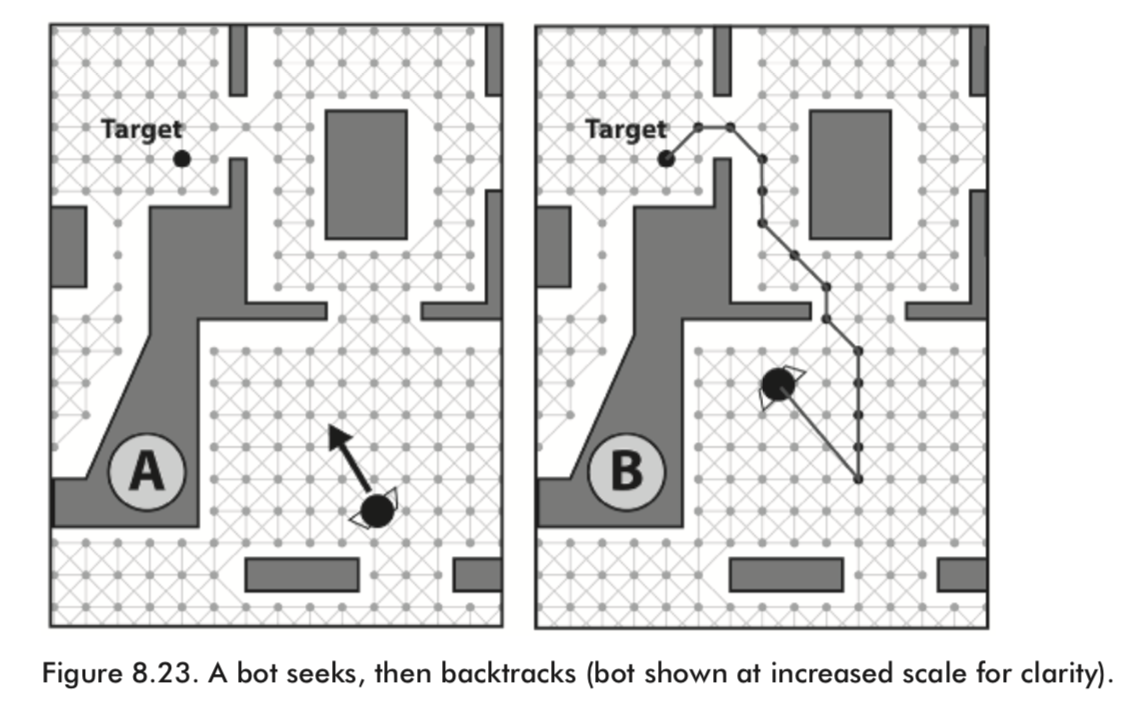
The above problem can be solved by combining time-sliced path planning with some sort of path smoothing.
Always the Same Path
If you see that your agents are often following each other in single file to reach a location or item, and you are utilizing A* to generate the paths, you can vary the path produced by the search algorithm by adding some noise to the heuristic. This will result in slightly different paths for the same search.
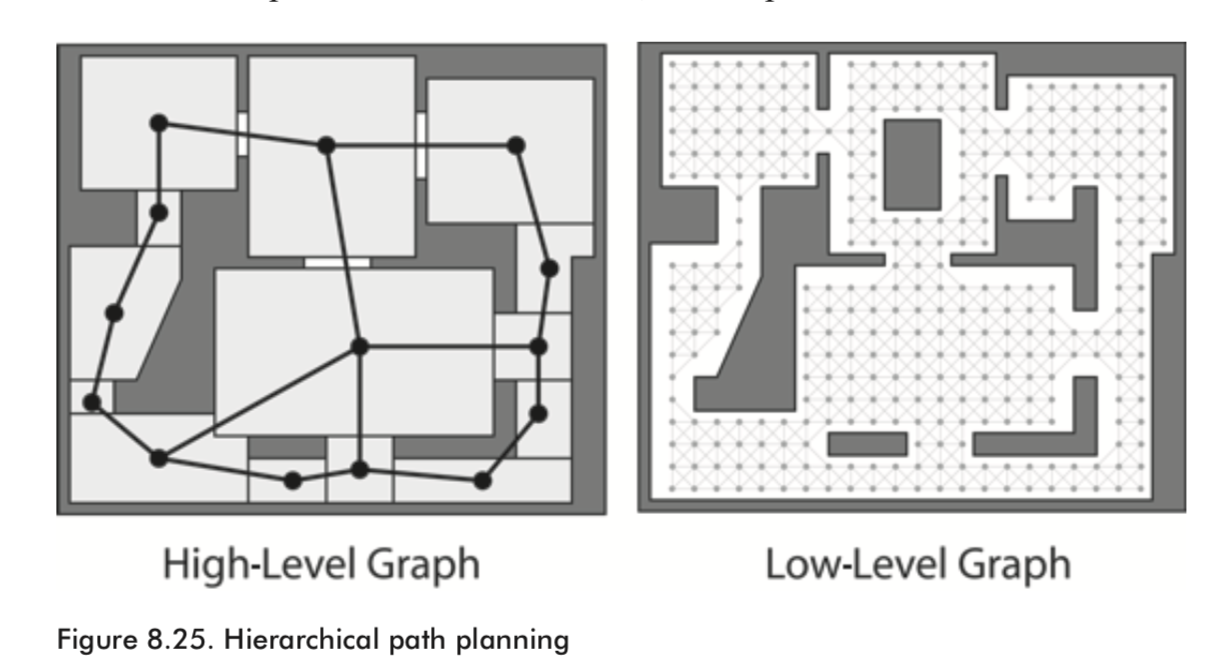
Hierarchical Pathfinding
Another technique available to cut down the CPU overhead of graph searches is named hierarchical pathfinding.
This concept can be replicated in a computer by designing a path planner that utilizes two superimposed navgraphs of different granularities — one coarse, one fine. The coarsely granulated graph deals with the high level, while the finely granulated graph deals with the low level. For example, in the game American Civil War, a hierarchical path planner for this game could utilize a coarsely granulated graph to represent connectivity information at the state level and a finely granulated one at the level of towns and roads. The planner then uses the finely grained navgraph to calculate paths between the states as and when the unit requires them. In this way searches of the finely grained graph are kept shallow, and therefore quick.
Getting Out of Sticky Situations
A problem players of computer games witness far too regularly is that of NPCs getting stuck. Given a simplest example, consider your agent is following a calculated path, and someone puts an obstacle in front of the agent. Then your agent will get stuck at that time, unless it recalculates the path again.
Therefore, to avoid this, one way is to calculate the distance to its current waypoint each update step. If this value remains about the same or consistently increases, then it’s a fair bet the agent is either stuck or being pushed backward by the separation force from neighboring agents.
Another way is to calculate an expected arrival time for each waypoint and replan if the current time exceeds the expected.