Maze generation algorithms are automated methods for the creation of mazes.

Graph Theory Based Methods

A maze can be generated by starting with a predeterminied arrangement of cells with wall sites between them. Then we apply specific algorithm to find a route between two particular nodes (making a subgraph).

If the subgraph is not connected, it means some regions are wasted.

If the subgraph contains loops, there can be multiple paths between the chosen space.

Because of the above two reasons, we usually generate mazes by generating a random spanning tree.

Depth First Search

This algorithm is a randomized version of the depth first search algorithm.

Start with a large grid of cells, each with four walls.
Select a random neighbouring cell that has not yet been visited.
Remove the wall between the two cells and marks the new cell as visited, and adds it to the stack to facilitate backtracking.
If a cell has no unvisited beighbors, it’s considered as a dead-end.
When at a dead-end it backtracks through the path until it reaches a cell with an unvisited neighbor, continuing the path generation by visiting new unvisited cell.

As given above this algorithm involves deep recursion which may cause stack overflow issues on some computer architectures. The algorithm can be rearranged into a loop by storing backtracking information in the maze itself.

Mazes generated with a depth-first search have a low branching factor and contain many long corridors, because the algorithm explores as far as possible along each branch before backtracking.

Randomized Kruskal’s Algorithm

This algorithm is a randomized version of Kruskal’s algorithm.

Create a list of all walls, and create a set for each cell, each containing just that one cell.
For each wall, in some random order. If the cells divided by this wall belong to distinct sets:
1. Remove the current wall.
2. Join the sets of the formerly divided cells.

Because the effect of this algorithm is to produce a minimal spanning tree from a graph with equally weighted edges, it tends to produce regular patterns which are fairly easy to solve.

Randomized Prim’s Algorithm

This algorithm is a randomized version of Prim’s algorithm.

Start with a grid full of walls.
Pick a cell, mark it as part of the maze. Add the walls of the cell to the wall list.
While there are walls in the list:
1. Pick a random wall from the list. If only one of the two cells that the wall divides is visited, then:
  1. Make the wall a passage and mark the unvisited cell as part of the maze.
  2. Add the neighboring walls of the cell to the wall list.
2. Remove the wall from the list.

Note that simply running classical Prim’s on a graph with random edge weights would create mazes stylistically identical to Kruskal’s, because they are both minimal spanning tree algorithms. Instead, this algorithm introduces stylistic variation because the edges closer to the starting point have a lower effective weight.

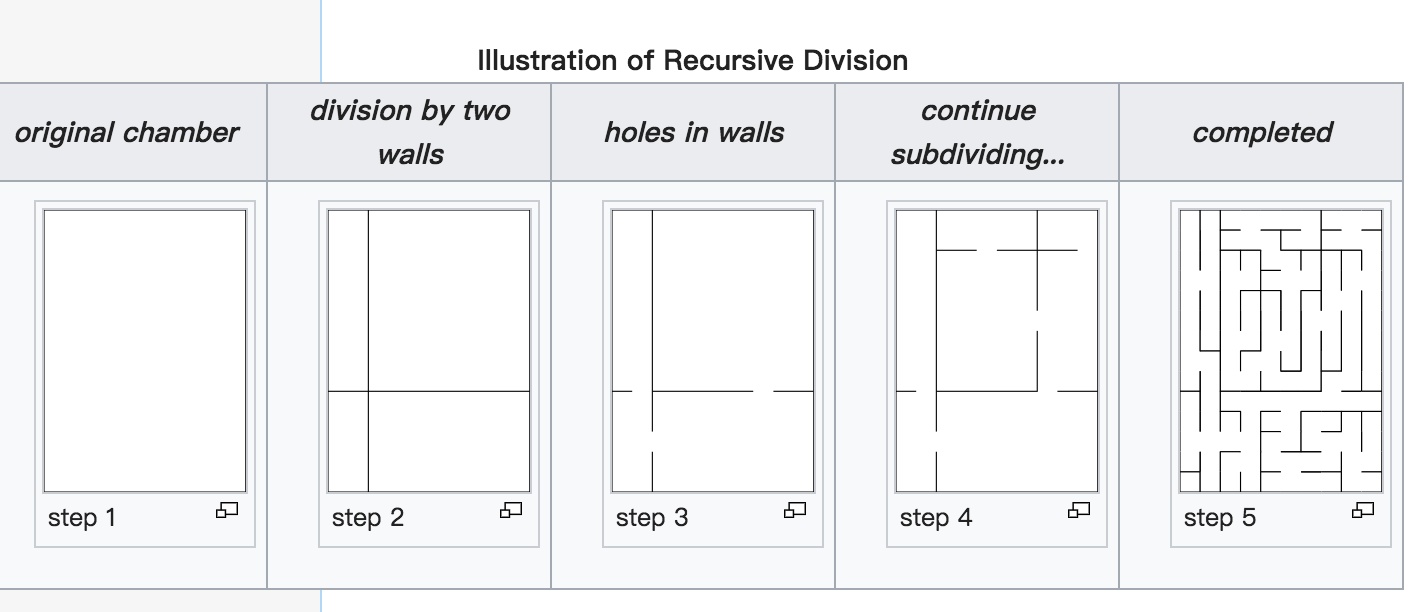
Recursive Division Method

Mazes can be created with recursive division, an algorithm which works as follows: Begin with the maze’s space with no walls. Call this a chamber. Divide the chamber with a randomly positioned wall (or multiple walls) where each wall contains a randomly positioned passage opening within it. Then recursively repeat the process on the subchambers until all chambers are minimum sized. This method results in mazes with long straight walls crossing their space, making it easier to see which areas to avoid.

Other Algorithms

Other algorithms exist that require only enough memory to store one line of a 2D maze or one plane of a 3D maze. They prevent loops by storing which cells in the current line are connected through cells in the previous lines, and never remove walls between any two cells already connected.

Code

Realization in Unity can be found in my github, including DFS and Prim’s Algorithm.

Conclusion

DFS: Long corridors.
Kruskal: Regular patterns.
Prim: Stylistically like Kruskal.
Recursion Division: Less corners to turn.