This is the reading note after reading
Here is the part of the Chapter 5.
Graph
Graph is commonly used in Game AI. Here I don’t give much details to what is a graph. I just give two examples about how graph is used in Game AI.
Example 1 : Navigation
A navigation graph, or navgraph, is an abstraction of all the locations in a game environment the game agents may visit and of all the connections between those points. Consequently, a well-designed navgraph is a data structure embodying all the possible paths through the game environment and is therefore extremely handy for helping your game agents decide how to get from A to B.
Each node in a navgraph usually represents the position of a key area or object within the environment and each edge represents the connections between those points. Furthermore, each edge will have an associated cost, which in the simplest case represents the distance between the nodes it con- nects. This type of graph is known to mathematicians as a Euclidian graph.
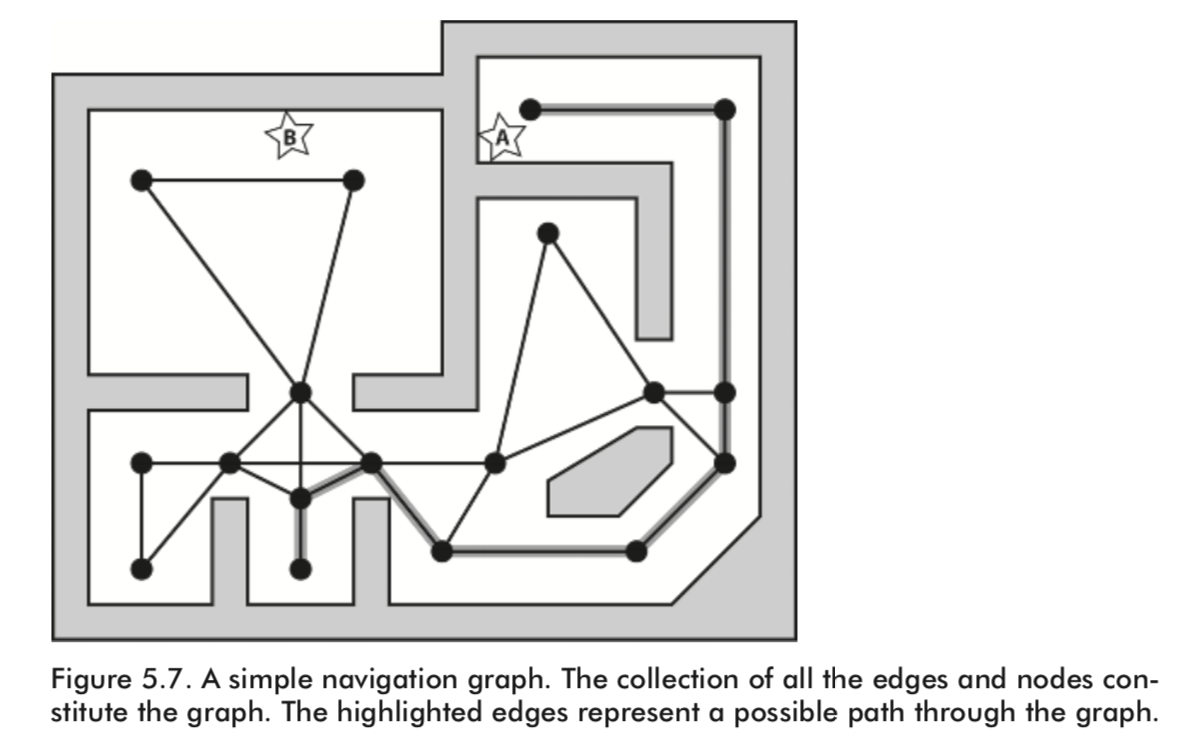
I’d like to make it clear that a game agent is not restricted to moving along the graph edges as though it were a train traveling along rails. An agent can move to any unobstructed position within the game environment, but it uses the navigation graph to negotiate its environment — to plan paths between two or more points and to traverse them. For example, if an agent positioned at point A finds it necessary to move to position B, it can use the navgraph to calculate the best route between the nodes closest to those points.
Example 2 : Dependency Graph
Dependency graphs are used in resource management type games to describe the dependencies between the various buildings, materials, units, and technologies available to a player.
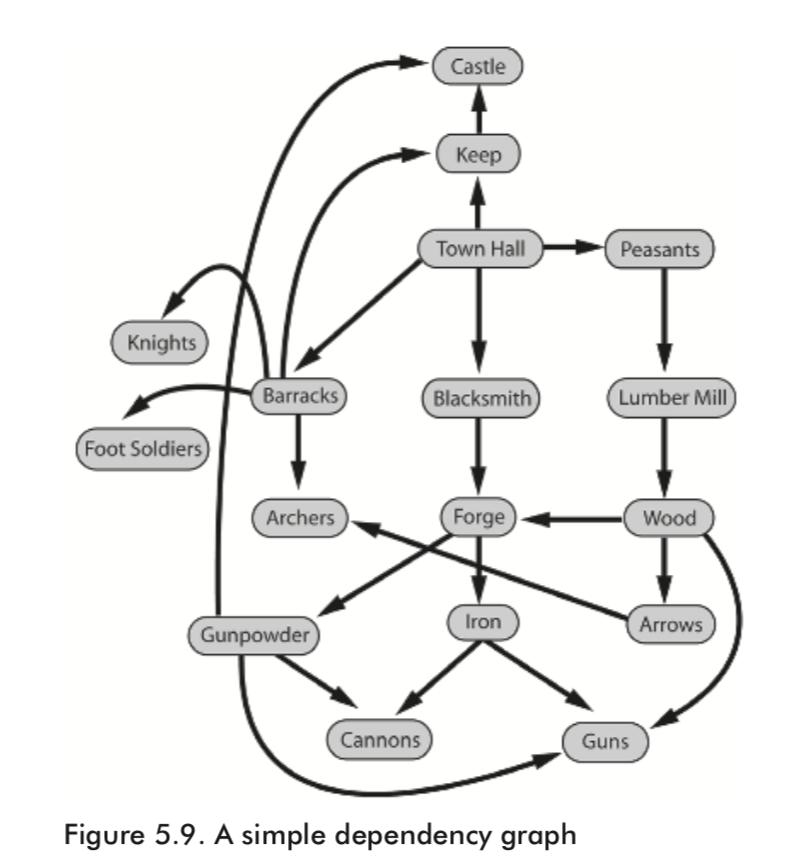
Dependency graphs are invaluable when designing an AI for this type of genre because the AI can use them to decide on strategies, predict the future status of an opponent, and assign resources effectively. Here are some examples based upon the graph shown in the figure.
- If the AI is preparing for battle and ascertains that archers are going to be advantageous, it can examine the dependency graph to conclude that before it can produce archers, it must first make sure it has a bar- racks and the technology of arrows. It also knows that in order to produce arrows it must have a lumber mill producing wood. There- fore, if the AI already has a lumber mill it can assign resources to building a barracks or vice versa. If the AI has neither a barracks nor a lumber mill it can inspect the technology graph further to determine that it’s probably advantageous to build the barracks before the lumber mill. Why? Because the barracks is a prerequisite for three different kinds of fighting unit, whereas a lumber mill is only a prerequisite for producing wood. The AI has already determined a battle is imminent, so it should realize (if you’ve designed it correctly, of course) that it should be putting resources into making fighting units as soon as pos- sible, because as we all know, knights and foot soldiers make better warriors than planks of wood!
- If an enemy foot soldier carrying a gun comes into the AI’s territory, the AI can work backward through the graph to conclude that:
- The enemy must have already built a forge and a lumber mill.
- The enemy must have developed the technology of gunpowder.
- The enemy must be producing the resources of wood and iron.
Further examination of the graph would indicate that the enemy probably either has cannons or is currently building them. Nasty!
The AI can use this information to decide on the best plan of attack. For example, the AI would know that to prevent any more gun-toting enemies from reaching its territory, it should target the enemy’s forge and lumber mill. It can also infer that sending an assas- sin to hit the enemy blacksmith would weaken its foe considerably, and perhaps devote resources toward creating an assassin for this purpose.
- Often, a technology or specific unit is key to a team winning a game. If the costs of building each resource are assigned to the dependency graph’s edges, then the AI can use this information to calculate the most efficient route to produce that resource
Graph Search
The following algorithms is about graph search. Graph search means given a source node and a target node, how we can find a path with minimum cost from the source to the destination.
Depth First Search
The depth first search is so named because it searches by moving as deep into the graph as possible. When it hits a dead end it backtracks to a shallower node where it can continue its exploration.
Pseudocode1
2
3
4
51 procedure DFS(G,v):
2 label v as discovered
3 for all edges from v to w in G.adjacentEdges(v) do
4 if vertex w is not labeled as discovered then
5 recursively call DFS(G,w)
The above pseudocode is for traversing the whole graph. If we want to use it the find a path, just start it from the source node and stop it when we reach the target node.
By DFS, we can always obtain the path from sourth to target if it exists one. However, we cannot get the path with minimum cost because we don’t consider cost in our algorithm and once we reach the target we stop the process and backtrack the path.
The time complexity is Θ(|V| + |E|), linear in the size of the graph. It’s not much efficient because as the number of nodes grows, the number of edges can be enormous. We can use it to traverse an entire graph and tells the accessibility of each node in the graph. But it’s not recommended to use it for searching a path in every frame.
More details can be found in wiki
Also there is one interesting application: Using DFS to generate a maze
Breadth First Search
The BFS algorithm fans out from the source node and examines each of the nodes its edges lead to before fanning out from those nodes and exam- ining all the edges they connect to and so on. You can think of the search as exploring all the nodes that are one edge away from the source node, then all the nodes two edges away, then three edges, and so on until the target node is found. Therefore, as soon as the target is located, the path leading to it is guaranteed to contain the fewest edges possible.
**Pseudocode1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55def breadth_first_search(problem):
# a FIFO open_set
open_set = Queue()
# an empty set to maintain visited nodes
closed_set = set()
# a dictionary to maintain meta information (used for path formation)
meta = dict() # key -> (parent state, action to reach child)
# initialize
root = problem.get_root()
meta[root] = (None, None)
open_set.enqueue(root)
#For each node on the current level expand and process, if no children (leaf, then unwind)
while not open_set.is_empty():
subtree_root = open_set.dequeue()
#We found the node we wanted so stop and emit a path.
if problem.is_goal(subtree_root):
return construct_path(subtree_root, meta)
#For each child of the current tree process
for (child, action) in problem.get_successors(subtree_root):
#The node has already been processed, so skip over it
if child in closed_set:
continue
#The child is not enqueued to be processed, so enqueue this level of children to be expanded
if child not in open_set:
#create metadata for these nodes
meta[child] = (subtree_root, action)
#enqueue these nodes
open_set.enqueue(child)
#We finished processing the root of this subtree, so add it to the closed set
closed_set.add(subtree_root)
#Produce a backtrace of the actions taken to find the goal node, using the recorded meta dictionary
def construct_path(state, meta):
action_list = list()
while True:
row = meta[state]
if len(row) == 2:
state = row[0]
action = row[1]
action_list.append(action)
else:
break
action_list.reverse()
return action_list
The time complexity can be expressed as {\displaystyle O(|V|+|E|)} O(|V|+|E|), since every vertex and every edge will be explored in the worst case. Like DFS, it’s not efficient in searching a path, or in small search space.
In BFS, we treat all edges as one-cost edge. Therefore we can only obtain the shortest path if that’s real(all edges with same cost).
Also, the path shape is entirely dependent on the order in which each node’s edges are explored.
More details can be found in wiki
Dijkstra
Dijkstra algorithm allows us to find the shortest path in weighted graph in high efficiency.
Dijkstra’s algorithm builds a shortest path tree one edge at a time by first adding the source node to the SPT and then by adding the edge that gives the shortest path from the source to a node not already on the SPT. This process results in an SPT containing the shortest path from every node in the graph to the source node. If the algorithm is supplied with a target node, the process will terminate as soon as it is found. At the point the algorithm terminates, the SPT it has generated will contain the shortest path to the source node from the target node, and from every node visited during the search.
Pseudocode1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 1 function Dijkstra(Graph, source):
2
3 create vertex set Q
4
5 for each vertex v in Graph: // Initialization
6 dist[v] ← INFINITY // Unknown distance from source to v
7 prev[v] ← UNDEFINED // Previous node in optimal path from source
8 add v to Q // All nodes initially in Q (unvisited nodes)
9
10 dist[source] ← 0 // Distance from source to source
11
12 while Q is not empty:
13 u ← vertex in Q with min dist[u] // Node with the least distance
14 // will be selected first
15 remove u from Q
16
17 for each neighbor v of u: // where v is still in Q.
18 alt ← dist[u] + length(u, v)
19 if alt < dist[v]: // A shorter path to v has been found
20 dist[v] ← alt
21 prev[v] ← u
22
23 return dist[], prev[]
Like the BFS, Dijkstra’s algorithm examines an awful lot of edges. Wouldn’t it be great if the algorithm could be given hints as it progresses to nudge the search along in the correct direction? Well, luckily for us, this is possible. Let’s welcome AStar.
AStar
Dijkstra’s algorithm searches by minimizing the cost of the path so far. It can be improved significantly by taking into account, when putting nodes on the frontier, an estimate of the cost to the target from each node under consideration. This estimate is usually referred to as a heuristic, and the name given to the algorithm that uses this method of heuristically directed search is A* (pronounced ay-star). And jolly good it is too!
If the heuristic used by the algorithm gives the lower bound on the actual cost (underestimates the cost) from any node to the target, then A* is guaranteed to give optimal paths. For graphs that contain spatial informa- tion, such as navigation graphs, there are several heuristic functions you can use, the most straightforward being the straight-line distance between the nodes in question. This is sometimes referred to as the Euclidean distance.
A* proceeds in an almost identical fashion to Dijkstra’s search algo- rithm. The only difference is in the calculation of the costs of the nodes on the search frontier. The adjusted cost, F, to the node when positioned on the priority queue (the search frontier), is calculated as:
F = G + H
where G is the cumulative cost to reach a node and H is the heuristic esti- mate of the distance to the target.
Pseudocode1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38function A*(start,goal)
closedset := the empty set //已经被估算的节点集合
openset := set containing the initial node //将要被估算的节点集合,初始只包含start
came_from := empty map
g_score[start] := 0 //g(n)
h_score[start] := heuristic_estimate_of_distance(start, goal) //通过估计函数 估计h(start)
f_score[start] := h_score[start] //f(n)=h(n)+g(n),由于g(n)=0,所以省略
while openset is not empty //当将被估算的节点存在时,执行循环
x := the node in openset having the lowest f_score[] value //在将被估计的集合中找到f(x)最小的节点
if x = goal //若x为终点,执行
return reconstruct_path(came_from,goal) //返回到x的最佳路径
remove x from openset //将x节点从将被估算的节点中删除
add x to closedset //将x节点插入已经被估算的节点
for each y in neighbor_nodes(x) //循环遍历与x相邻节点
if y in closedset //若y已被估值,跳过
continue
tentative_g_score := g_score[x] + dist_between(x,y) //从起点到节点y的距离
if y not in openset //若y不是将被估算的节点
add y to openset //将y插入将被估算的节点中
tentative_is_better := true //暂时判断为更好
elseif tentative_g_score < g_score[y] //如果起点到y的距离小于y的实际距离
tentative_is_better := true //暂时判断为更好
else
tentative_is_better := false //否则判断为更差
if tentative_is_better = true //如果判断为更好
came_from[y] := x //将y设为x的子节点
g_score[y] := tentative_g_score //更新y到原点的距离
h_score[y] := heuristic_estimate_of_distance(y, goal) //估计y到终点的距离
f_score[y] := g_score[y] + h_score[y]
return failure
function reconstruct_path(came_from,current_node)
if came_from[current_node] is set
p = reconstruct_path(came_from,came_from[current_node])
return (p + current_node)
else
return current_node
AStar allows us to find a path from source to target in a relatively short time. And it’s also the most commonly used algorithm in game ai.
In practice, we can use different heuristics to represent different cost. For example, in a 4-connected grid map, it’s better to use manhattan heuristic. In a thief topic game, you need to use a heuristic considering the sound made by the move. Here is a link about the difference between Euclidean and Manhattan